Θαλής ο  Μιλήσιος (640-546 π.Χ)

Ο ιστορικός Ιερώνυμος (350-250 π.Χ.) και ο Πλούταρχος (46-126 μ.Χ.) αναφέρουν ότι ο Θαλής υπολόγισε το ύψος των Πυραμίδων της Αιγύπτου με τη βοήθεια της σκιάς τους και της σκιάς του μπαστουνιού του, αφήνοντας έκπληκτους τους σοφούς Αιγυπτίους ιερείς.

Το γεγονός αυτό συνέβη γύρω στο 565 π.Χ.  στην αρχή της βασιλείας του Φαραώ Άμαση (Βασίλεψε 569-525 π.Χ.)

Συγκεκριμένα ο Θαλής κάποιο μεσημέρι μέτρησε το μήκος της σκιάς της πυραμίδας και το μήκος της σκιάς που ρίχνει μια κατακόρυφη ράβδος. Γνωρίζοντας  τώρα ότι τα ύψη και οι αντίστοιχες σκιές είναι ανάλογα οδηγήθηκε στον υπολογισμό του ύψους της πυραμίδας.

Πυθαγόρας (580-500 π.Χ)

Πυθαγόρειο Θεώρημα

Το Θεώρημα ανακαλύφτηκε και αποδείχτηκε στο τέλος περίπου του 6 αι. π.Χ., στο περίφημο πανεπιστήμιο που είχε ιδρύσει ο Πυθαγόρας (580-500 π.Χ.) στον Κρότωνα .

Πιστεύεται δε ότι είναι έργο του ίδιου του Πυθαγόρα. Λέω πιστεύεται γιατί οι έρευνες του Πανεπιστημίου, για λόγους μυστικιστικούς, δεν δημοσιεύονταν, με αποτέλεσμα  οι πληροφορίες μας να προέρχονται από μεταγενέστερες πηγές.

Ενώ όμως  η επινόηση του Θεωρήματος ήταν κατάκτηση για την Γεωμετρία και τον πολιτισμό, για τους Πυθαγόρειους εμπνευστές του ήταν αφορμή για αμηχανία και εκνευρισμό.

Και αυτό γιατί κατά την εφαρμογή του, για τον υπολογισμό διαγωνίων ορθογωνίων παραλληλογράμμων, υψών ισοπλεύρων τριγώνων και άλλων μηκών, διαπίστωσαν ότι δεν υπάρχουν αριθμοί που να μπορέσουν να εκφράσουν αυτά τα μήκη.

Στο τετράγωνο, παραδείγματος χάριν, με μήκος πλευράς α=1 διαπίστωσαν ότι οι μέχρι τότε γνωστοί αριθμοί δεν μπορούσαν να εκφράσουν το μήκος της διαγωνίου του δ και αυτό γιατί το θεώρημα έδινε τη σχέση δ²=α²+α² ή την δ²=2.

Όμως τι αριθμός ήταν αυτός ο δ που το τετράγωνό του ήταν ίσο με 2 ; Τέτοιος αριθμός δεν υπήρχε ούτε ακέραιος ούτε κλασματικός.

Το σοκ ήταν ισχυρό γιατί οι Πυθαγόρειοι, που πίστευαν ότι η ουσία και η έκφραση των πάντων είναι οι αριθμοί, διαπίστωσαν ότι υπήρχαν τμήματα, όπως η διαγώνιος, που ενώ ήταν πλήρως αντιληπτά σαν μεγέθη, δεν μπορούσαν να εκφραστούν με τους τότε γνωστούς αριθμούς. Το αδιέξοδο αυτό, έθιγε ένα από τα βασικά δόγματα του Πυθαγορείου συλλόγου, πρέπει να προκάλεσε πλήθος συζητήσεων και μεγάλη αμηχανία.

Οι συζητήσεις αυτές έγιναν αφορμή να μπει στη Γεωμετρία η έννοια των ασυμμέτρων μεγεθών, δηλαδή μεγεθών που δεν έχουν κοινό μέτρο, και αργότερα να επινοηθεί μέθοδος για τον υπολογισμό των τετραγωνικών ριζών.

Η επινόηση μεθόδου για τον υπολογισμό τετραγωνικών ριζών κατορθώθηκε 150 χρόνια περίπου μετά την ανακάλυψη του Πυθαγορείου Θεωρήματος, από τον Αρχύτα τον Ταραντίνο (428-365 π.Χ.) τον τελευταίο των Πυθαγορείων.

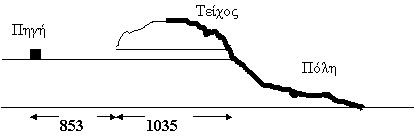
Ευπαλίνος

Ευπαλίνειο Όρυγμα

Στο τέλος του 6αι. π.Χ την εξουσία στη Σάμο πήρε από τους Αριστοκρατικούς ο Πολυκράτης. Αυτός κυβέρνησε το νησί σαν τύραννος από το 537-522 π.Χ.

Κατά τη διάρκεια της τυραννίας του εκτέλεσε μεγάλα έργα όπως το τείχος γύρω από την πόλη της Σάμου (σημερινό Πυθαγόρειο) το μεγάλο λιμενοβραχίονα  μήκους 360 μέτρων και βάθους στο άκρο του 36 μέτρων, το ναό της Ήρας διαστάσεων 108,70x52,40 μέτρων με 155 κίονες και το περίφημο υδραγωγείο της πόλης.

Οι προδιαγραφές που έβαλε ο Πολυκράτης για το υδραγωγείο ήταν :

1.    Να τροφοδοτείται από το νερό της πλούσιας πηγής των Αγιάδων.

2.    Να είναι υπόγειο με επισκέψιμα τα τμήματα του αγωγού.

3.    Να βράζει νερό σε ορισμένο σημείο εσωτερικό των τειχών και σε στάθμη υψηλότερη της τότε πόλης για την αβίαστη διανομή του.

Η πηγή όμως βρισκόταν πίσω από το βουνό, το οποίο αποτελούσε με τον όγκο του ανυπέρβλητο εμπόδιο στη ροή του νερού. Έτσι για την ασφαλή, σε περίπτωση πολιορκίας, ροή του νερού έπρεπε να τρυπηθεί το βουνό και να κατασκευασθεί μια σήραγγα  στην αρχή και το τέλος της.

Η κατασκευή του έργου ανατέθηκε στον αρχιτέκτονα Ευπαλίνο από τα Μέγαρα. Αυτός αφού έκανε τις αναγκαίες τοπογραφικές εργασίες για τον προσδιορισμό της διεύθυνσης και της κλίσης της σήραγγας άρχισε τις εργασίες της διάνοιξης και από τα δύο προκαθορισμένα άκρα της.

Τέτοια διάτρηση βουνού δεν είχε επιχειρηθεί ξανά από κανένα πολιτισμό και σε καμιά εποχή πριν από τον Ευπάλινο. Το τόλμημα ήταν ριψοκίνδυνο γιατί υπήρχε το ενδεχόμενο οι δυο σήραγγες από κακή χάραξη, να μην συναντηθούν ποτέ.

Τελικά οι δυο σήραγγες συναντήθηκαν με πολύ μικρή απόκλιση από την ευθεία. Το συνολικό μήκος της διάτρησης είναι 1035 μ. (Κατά τον Ηρόδοτο 7 στάδια = 1294 μ.) Από αυτά τα 615 μ. είναι το μήκος της βόρειας σήραγγας και τα 420 της νότιας. Η απόκλιση από την ευθεία των δυο σηράγγων  ήταν μόλις  6 μ. Το πλάτος της σήραγγας είναι περίπου 2,30 μ. και το ύψος 1,90. Στο δάπεδο της σήραγγας υπάρχει αυλάκι μέσα στο οποίο ήταν τοποθετημένοι οι πήλινοι σωλήνες που έφεραν το νερό. Η διάτρηση του βουνού διάρκησε περίπου 6 χρόνια ενώ η εκτέλεση και των άλλων έργων (τάφρος, σωληνώσεις κ.λ.π) πρέπει να ολοκληρώθηκε σε 10 χρόνια περίπου.

Το υδραγωγείο του Ευπαλίνου λειτούργησε μέχρι τον 5 αι. μ.Χ γύρω στα 1000 χρόνια. Μετά φαίνεται στέρεψε η πηγή του, έπαψε η συντήρησή του και καταχώθηκε από χώματα. Η οριστική του αποκατάσταση του και ο καθαρισμός του από άλλα υλικά έγινε το 1971 από το Γερμανικό αρχαιολογικό Ινστιτούτο.

Αν και σήμερα είναι άγνωστη η γεωμετρική διαδικασία που ακολουθήθηκε για τη χάραξη της διάτρησης το ότι το έργο ολοκληρώθηκε μπορούμε να πούμε σήμερα ότι τότε γνώριζαν πολύ περισσότερα από όσα εμείς γνωρίζουμε για τις γνώσεις της εποχής εκείνης.

Μας βεβαιώνει ότι ο Ευπαλίνος , γύρω στο 530 π.Χ γνώριζε :

Το Πυθαγόρειο Θεώρημα

Τον υπολογισμό των τετραγωνικών ριζών

Τις έννοιες ΛΟΓΟΣ, ΑΝΑΛΟΓΙΑ, ΟΜΟΙΟΤΗΤΑ.

ΗΡΩΝΑΣ Ο ΑΛΕΞΑΝΔΡΕΥΣ

Αλεξάνδρεια 65 μ.Χ. -125 μ.Χ.

Περίφημος Γεωμέτρης και μηχανικός. Το Ι βιβλίο του, από τη διατριβή του την Μετρική ασχολείται με εμβαδά τριγώνων, τετραπλεύρων, κανονικών πολυγώνων, από 2 έως 12 πλευρές, επιφάνειες κώνων, κυλίνδρων, πρισμάτων, πυραμίδων, σφαιρών κ.λ.π. Εξετάζεται επίσης μία μέθοδος γνωστή στους Βαβυλωνίους 2000 χρόνια πριν, για την προσέγγιση της τετραγωνικής ρίζας ενός αριθμού.

Ο Ήρωνας επίσης αποδεικνύει την περίφημη φόρμουλα που δίνει το εμβαδόν του τριγώνου βάσει της ημιπεριμέτρου , Ε= [s(s-a)(s-b)(s-c)]1/2 όπου s=( a+b+c)/2.

Στο ΙΙ βιβλίο Μετρικής ο Ήρωνας ασχολείται με όγκους τρισδιάστατων σχημάτων όπως σφαίρες, κυλίνδρους, κώνους, πρίσματα, πυραμίδες κ.λ.π.

Στο ΙΙΙ βιβλίο Μετρικής ασχολείται με το διαχωρισμό εμβαδών και όγκων σύμφωνα με μία δοθείσα αναλογία.

Στο βιβλίο του Διόπτρα ασχολείται με θεοδολίχους και τοπογραφήσεις. Περιλαμβάνει επίσης ένα κεφάλαιο αστρονομίας που δίνει την μέθοδο να βρεις την απόσταση μεταξύ Αλεξάνδρειας και Ρώμης χρησιμοποιώντας την διαφορά μεταξύ της τοπικής ώρας κατά την οποία παρατηρήθηκε μία έκλειψη της σελήνης από την κάθε πόλη.

Στο βιβλίο του περί Κατόπτρων ασχολείται με τους καθρέφτες. Ο Ήρωνας στη μελέτη του για το φως αναφέρει ότι τα αποτελέσματα της όρασης από τις ακτίνες φωτός εκπορεύονται από τα μάτια. Πιστεύει ότι αυτές οι ακτίνες ταξιδεύουν με άπειρη ταχύτητα.

Ο Ήρωνας έγραψε πολλά σπουδαία πράγματα πάνω στη Μηχανική . Έδωσε μεθόδους ανύψωσης μεγάλων σε βάρος αντικειμένων καθώς επίσης κατασκεύασε αυτόματα μηχανήματα και υδραυλικά ρολόγια. Είναι ο πρώτος που κατασκεύασε ατμοκίνητη μηχανή. Γνωστή είναι επίσης η Κρήνη του Ήρωνα μία συσκευή με την οποία δημιουργείται πίδακας με την δύναμη πιεσμένου αέρα που προέρχεται από ροή νερού μέσα σε κλειστό χώρο.

ΥΠΑΤΙΑ

Αλεξάνδρεια 370 μ.Χ. - 415 μ.Χ.

Η Υπατία υπήρξε από τις πιο εξιδανικευμένες μορφές της επιστήμης. Ήταν κόρη του Θέωνα, την γνωρίζουμε δε μέσα από τα γράμματά της. Υπήρξε πολυταξιδεμένη. Αλληλογραφούσε με πολύ κόσμο από την περιοχή της Μεσογείου. Δίδαξε στην φιλοσοφική σχολή του της Αλεξάνδρειας μαθηματικά και φιλοσοφία. Διακρίθηκε στην Άλγεβρα στην Αστρονομία και τη Γεωμετρία. Εφηύρε ορισμένα εργαλεία όπως ένα όργανο για την διύλιση του νερού και την πλανισφαίρα.

Πέθανε βίαια, πιθανόν συρόμενη μέσα στους δρόμους από ένα όχλο που την εκτέλεσε με κελύφη από όστρακα. Περιγράφεται ο θάνατός της περισσότερο σαν πολιτική δολοφονία παρά σαν κάτι που έγινε από ένα εξοργισμένο όχλο. Υπονοείται ότι η Υπατία βρέθηκε στο μέσον ενός ανταγωνισμού ανάμεσα στον Κύριλο, αρχιεπίσκοπο της Αλεξάνδρειας, και του Ορέστη πολιτικό αρμόδιο της πόλης που τοποθετήθηκε σε αυτή τη θέση λίγο μετά τον Κύριλο. Η Υπατία ήταν με την πλευρά του Ορέστη. Η επιρροή της ήταν τόσο μεγάλη που υπονόμευσε τον Κύριλο και τον παρακίνησε εναντίον της επιφέροντας τελικά τον θάνατό της.

Αυτή έγραψε ότι οι δογματικές θρησκείες είναι λανθασμένες και από αυτοσεβασμό και μόνο δεν πρέπει να γίνονται αποδεκτές. Κράτησε το δικαίωμά σου από το να μη σκέφτεσαι καθόλου να σκέφτεσαι λάθος. Είναι φοβερό πράγμα να διδάσκεις δεισιδαιμονίες για αλήθειες.

ΕΡΑΤΟΣΘΕΝΗΣ

(Μαθηματικός και Γεωγράφος ) από την Κυρήνη (290-205 π.Χ.)

Ο Ερατοσθένης όμως διακρίθηκε και θαυμάστηκε κυρίως ως γεωγράφος. Ζητούσε να βρει το μήκος του μεσημβρινού της Γης κι έτσι θα μπορούσε να βρει την ακτίνα της γήινης σφαίρας.

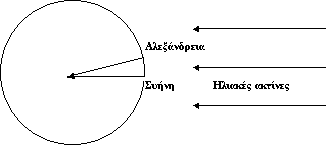
Το 250 π.Χ. παρατήρησε ότι στην πόλη Συήνη (σημερινό Ασουάν) που βρίσκεται 800 km περίπου νότια της Αλεξάνδρειας, ο Ήλιος καθρεφτιζόταν το μεσημέρι της αρχής του καλοκαιριού (22 Ιουνίου) στα νερά των πηγαδιών, γεγονός που σήμαινε ότι βρισκόταν στο ζενίθ του τόπου. Την ίδια ώρα ο οβελίσκος της Αλεξάνδρειας έδινε σκιά 7^ο,5 .

Θεωρώντας ότι οι ακτίνες του Ηλίου είναι παράλληλες και στον τύπο:

έθεσε μ=800 km και τ=7^ο,5 , οπότε βρήκε το μήκος της περιφέρειας της γης στη συνέχεια

κάνοντας χρήση Μ=2πR υπολόγισε την ακτίνα της γης R

Αθανασιάδης Αθανάσιος

athanasiadi@sch.gr